

Swing the pencil leg of the compass to make a tiny mark through that second arc.
Put the point down on the intersection of the second arc and the transverse ( P o i n t U in our example). Lift the compass, being careful to keep the legs the same distance apart. Open or close the compass leg to match the distance from that intersection to the arc's other intersection, where it crosses the horizontal line ( L D in our example). You will put the compass's sharp point on the intersection of the first arc you drew and the transverse. Lift the compass and do not worry about the distance between the legs. Scribe another arc to look similar to the one you just drew. Keep the compass legs the same distance apart and repeat the arc with the compass's sharp point on P o i n t U. Put the point of the compass on P o i n t E and scribe an arc that goes through the transverse line and the horizontal line (in our example, lines U E and L D). In our example, the compass is spread slightly more than halfway between P o i n t U and P o i n t E. Open the compass legs so that they are more than half the distance from the two points on your transverse. So far, we have line L D intersected by transverse U E. Label the intersection of your transverse and your original line with another letter not already used. Next, we will use our straightedge to construct a transverse, a line intersecting your original line and going through your point above the line. Label the points of your line anything you like the letters are unimportant except to identify your line.įor our example, we will construct line L D.ĭraw a single point above your line, some distance away (like 3 inches) and give it a label. Now, let’s look at alternate exterior angles.Įxterior means outside and alternate means opposite sides of the transversal.Īlternate exterior angles are also congruent.How To Construct A Parallel Line Through A Point Step 1īegin by drawing a line (or ray or line segment) horizontally on your paper, relative to you. These angles are also congruent.Īngle and are also alternate interior angles.
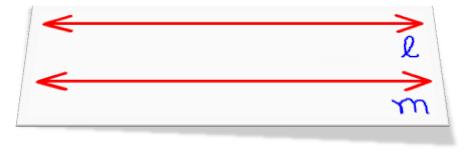
While interior means in between the parallel lines. If we go from one side of the transversal to the other, that’s called an alternate.Īngles on one side of the transversal are called same-side.Īlternate means the different side of the transversal. Those that are outside of this are known as exterior angles. And so on.Īngles in between the two parallel lines are called interior angles. Which makes them congruent with each other.Ĭorresponding angles are angles that match up on the diagram. So, we can say that these two are congruent.įinally, angle is on the bottom right just like angle. Now, let’s look at the angle, which is at the bottom left same as angle. Likewise, angle is on the top right as well as angle. Meaning they have the same exact measurement. Which means they have the same exact measurement.Īngles and are corresponding angles so they are congruent. Now if we focus on the bottom line and transversal, angles formed here corresponds to the angles formed by the top line.Īngles that corresponds to a group are called corresponding angles. When a transversal intersects two parallel lines, there are a lot of angle relationships that result.įirst, if we ignore the bottom line and focus on the top line and transversal, there are already a lot of angles. We also have line which is the transversal. We have lines and which are parallel to each other. In this lesson, we’ll go over angle relationships resulting from two parallel lines cut by a transversal. Graphically, they face the same way and are all always congruent.

Same-side Exterior Angles: Angles that are outside on different sides of the two parallel lines, but are on the same side of the transversal.Same-side Interior Angles: Angles in between the parallel lines and on the same side of the transversal.Alternate Exterior Angles: Angles that are outside on different sides of the two parallel lines, and are on different sides of the transversal.Alternate Interior Angles: – Angles that are between the two parallel lines, but are on opposite sides of the transversal.Supplementary Angles: – Two angles that always add up to.Vertical Angles: – Angles formed by intersecting lines opposite of each other and are also congruent.Here is a list of commonly used terms to describe angles formed by two parallel lines that are cut by a transversal.


 0 kommentar(er)
0 kommentar(er)
